图像处理lab2

lzf 发布于

文章访问量

图像处理lab2

21371255 刘兆丰

1.Questions

1.1 corner detection

“corners”（角点）指的是图像中具有明显边缘或纹理变化的位置。角点通常是图像中的一些重要特征点，因为它们在不同图像之间具有较高的稳定性和可重复性。

（a）使用 Harris corner detection

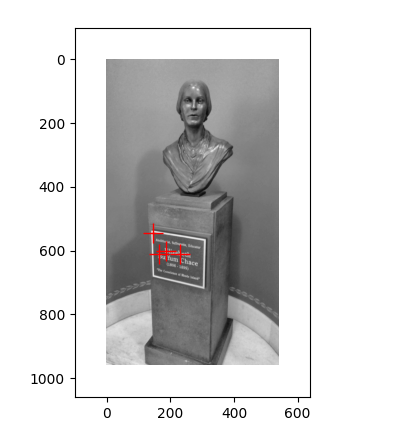
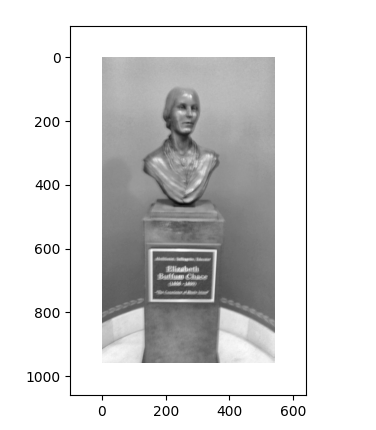
pair 1:

image-20240505143423293.png

image-20240505143534351.png

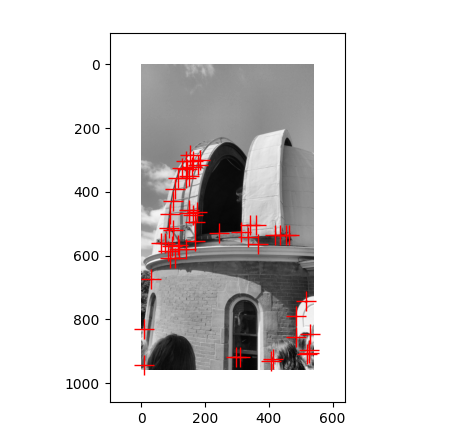
pair2:

image-20240505143600713.png

image-20240505143622592.png

pair3:

image-20240505143718398.png

image-20240505143751673.png

（b）

pair1 ：第一张图检测到了雕像上的角点，但第二张图没有检测到角点，可能是因为第二张图片较为模糊的原因

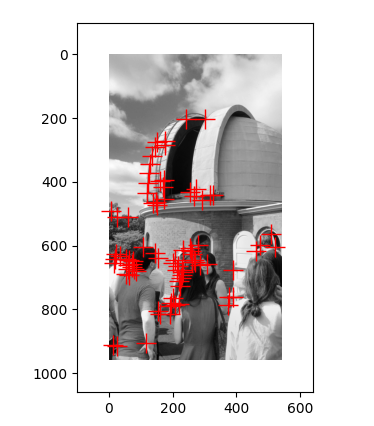
pair2： 两张图都检测到了建筑上的角点，但是第二张图相比第一张图，多检测了底下人身上的角点，说明周围环境会影响角点的检测

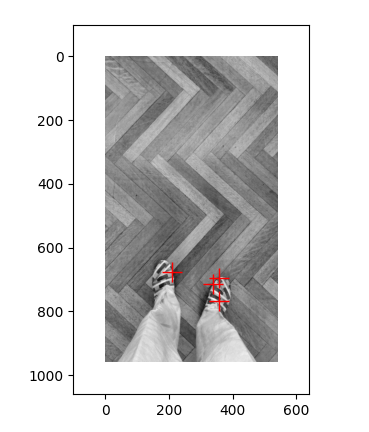
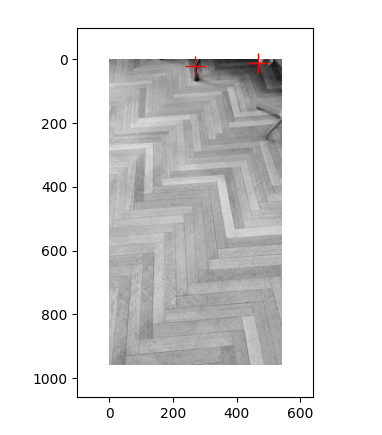
pair3： 第一张图检测的是鞋子上的角点，第二张图检测的是旁边的椅子的腿，可能是因为图中突出部位的不同导致了检测角点的不同

图像特征匹配的挑战：

视点变化：当图像从不同的视角或观察点捕获时，特征点的外观和位置可能发生变化。这导致了特征点在不同图像之间的不精确匹配。

光照变化：光照条件的变化会导致图像中的亮度、对比度和颜色发生变化。这会影响特征点的外观，使得在不同光照条件下进行特征匹配变得困难。

遮挡：图像中的物体遮挡可能导致一些特征点无法在不同图像中被观察到。这会导致匹配算法无法找到正确的对应关系。

尺度变化：当物体在图像中发生尺度变化时，特征点的大小和分布也会发生变化。这对于尺度不变的特征描述子来说是一个挑战，因为它们需要在不同尺度之间进行匹配。

噪声和图像失真：图像中的噪声、模糊或压缩失真会导致特征点的检测和描述变得困难。这可能会导致特征匹配的错误或不准确。

重复纹理：当图像中存在大量重复纹理时，特征点的选择和匹配变得困难。重复纹理可能导致特征点之间的混淆和模糊。

1.2 Distance metrics for feature matching

特征匹配中的距离度量（distance metrics）是用于衡量特征描述子之间的相似性或差异性的方法。在特征匹配过程中，通过计算描述子之间的距离，可以确定最佳匹配的特征点对。

（a）

欧氏距离（Euclidean Distance）：欧氏距离是最简单和常用的距离度量方法。对于两个特征描述子向量x和y，欧氏距离可以通过计算它们之间的欧氏距离来衡量：

d(x, y) = sqrt(sum((x[i] - y[i])^2))，其中i表示向量的维度。

余弦相似度（Cosine Similarity）：余弦相似度是一种衡量向量相似性的度量方法。对于两个特征描述子向量x和y，余弦相似度可以通过计算它们之间的夹角余弦来衡量：

similarity(x, y) = (x·y) / (||x|| * ||y||)，其中·表示向量的点积，||x||和||y||表示向量的范数。

根据这些几何解释，我们可以了解到何时使用每种度量方法：

欧氏距离适用于考虑向量大小和方向的情况。当特征描述子的绝对值和相对位置对于任务很重要时，欧氏距离是一个合适的选择。例如，在图像处理中，当我们关注特征点的位置和形状时，欧氏距离可以用于匹配和跟踪特征点。

余弦相似度适用于只考虑向量方向的情况。当特征描述子的绝对值不重要，而我们关注特征之间的方向性和趋势时，余弦相似度是一个合适的选择。例如，在文本分类中，我们可以使用余弦相似度来计算文档之间的相似性，而不考虑文档的长度或词频。

（b）

好的特征描述子匹配方法应具备以下特点：

鲁棒性（Robustness）：好的方法应对图像变化、噪声和遮挡等因素具有鲁棒性。它应能够识别出相似的特征，即使在图像中存在略微的变化或干扰。

精确性（Accuracy）：好的方法应能够准确地匹配相应的特征描述子，以确保匹配结果的准确性。它应该能够准确地区分出最佳匹配和误匹配。

效率（Efficiency）：好的方法应具备高效的计算性能，特别是在大规模数据集和实时应用中。它应该能够在合理的时间内完成匹配任务，以满足实际应用的要求。

可扩展性（Scalability）：好的方法应具备可扩展性，能够应对不同规模和复杂度的数据集。它应该能够处理大量的特征描述子，并能够在不同场景和数据集上进行泛化。

适应性（Adaptability）：好的方法应具备适应不同类型和特征描述子的能力。它应该能够处理不同种类的特征描述子，如局部特征、全局特征或深度学习特征。

非刚性匹配（Non-rigid Matching）：好的方法应具备处理非刚性形变的能力，例如目标变形、姿态变化或形状扭曲等。它应能够捕捉到非刚性变换下的相似性。

1.3 homography

（a)首先，将点y = λn + x表示为齐次坐标形式，即[Y, W] = [λa + u, λb + v, λ]。

然后，通过矩阵乘法运算，将新的点y’表示为：

1
2
3
4
5
6
7
8
[Y', W'] = H * [Y, W] 
= [h11(λa + u) + h12(λb + v) + h13λ]
  [h21(λa + u) + h22(λb + v) + h23λ]
  [h31(λa + u) + h32(λb + v) + h33λ]

= [h11λa + h12λb + h13λ + h11u + h12v]
  [h21λa + h22λb + h23λ + h21u + h22v]
  [h31λa + h32λb + h33λ + h31u + h32v]

将新的点y’转换回笛卡尔坐标形式，得到线ℓ’：

$(\frac{h11λa + h12λb + h13λ + h11u + h12v}{h31λa + h32λb + h33λ + h31u + h32v},\frac{h21λa + h22λb + h23λ + h21u + h22v}{h31λa + h32λb + h33λ + h31u + h32v})$

(b) 要计算消失点y’v，可以考虑当λ → ∞ 时的点[Y’, W’]的极限。

当$h31a + h32b + h33!=0$ 且

$h31a + h32b + h33!=0$ 时，收敛到一个消失点

$y^{,}_v $= lim(λ→∞) ℓ’ = $(\frac{h11a + h12b + h13 }{h31a + h32b + h33},\frac{h21a + h22b + h23}{h31a + h32b + h33})$

（c） 当$h31a + h32b + h33=0$ 或

$h31a + h32b + h33=0$ 时，不会收敛到一个消失点

2.Programming

1. 代码

1.get_interest_points()
  1. 计算梯度：使用Sobel算子计算图像的水平和垂直梯度，分别保存在grad_x和grad_y中。
  2. 平滑梯度：对计算得到的梯度图像进行高斯平滑以减少噪声。
  3. 计算结构张量：利用平滑后的梯度计算结构张量的各个分量（Ixx、Iyy、Ixy）。
  4. 计算Harris响应：使用结构张量计算Harris响应函数，即通过对结构张量进行运算得到每个像素点的Harris响应值。这里使用了一个窗口（kernel）来计算每个像素点的Harris响应。
  5. 非极大值抑制：在Harris响应图上执行非极大值抑制，以便仅保留局部最大的响应值，以确定兴趣点的位置。
  6. 边界过滤：滤除位于图像边界附近的兴趣点，因为边界附近的响应值可能受限于窗口的大小，不够准确。

最后，返回有效的兴趣点的坐标（xs和ys），这些坐标是经过非极大值抑制和边界过滤后剩余的兴趣点的位置。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def get_interest_points(image, feature_width):

    # Step 1: Compute gradients
    grad_x = sobel_h(image)
    grad_y = sobel_v(image)

    # Step 2: Smooth gradients to reduce noise
    grad_x_smooth = gaussian(grad_x, sigma=1)
    grad_y_smooth = gaussian(grad_y, sigma=1)

    # Step 3: Compute the structure tensor
    Ixx = grad_x_smooth ** 2
    Iyy = grad_y_smooth ** 2
    Ixy = grad_x_smooth * grad_y_smooth

    # Step 4: Compute the Harris response
    kernel = np.ones((feature_width, feature_width))
    Sxx = convolve(Ixx, kernel)
    Syy = convolve(Iyy, kernel)
    Sxy = convolve(Ixy, kernel)

    det = Sxx * Syy - Sxy ** 2
    trace = Sxx + Syy
    harris_response = det - 0.04 * trace ** 2  # 0.05 is an empirical constant

    # Step 5: Apply non-maximum suppression
    corners = peak_local_max(harris_response, min_distance=feature_width, threshold_rel=0.01)

    # Step 6: Filter out points near the image boundaries
    valid_corners = []
    height, width = image.shape
    for corner in corners:
        y, x = corner
        if feature_width <= x < width - feature_width and feature_width <= y < height - feature_width:
            valid_corners.append(corner)

    xs = np.array([corner[1] for corner in valid_corners])
    ys = np.array([corner[0] for corner in valid_corners])

    return xs, ys
2. get_features()
  1. 基于灰度图像的方法（注释部分）：
    • 首先，对于每个兴趣点，提取其周围的图像块（patch）。
    • 将提取的图像块进行归一化处理，将像素值范围映射到0到1之间。
    • 将归一化的图像块展平为一维数组，作为特征描述符。
    • 所有特征描述符存储在一个列表中，并最终转换为NumPy数组。
  2. 基于SIFT的方法：
    • 对于每个兴趣点，提取其周围的图像块。
    • 将图像块分割为4x4个单元格（cells）。
    • 对于每个单元格，计算其梯度和方向。
    • 将每个单元格的梯度方向分成8个方向的直方图（每个方向45度），并根据梯度幅值加权。
    • 将所有单元格的直方图连接成一个特征向量。
    • 对特征向量进行归一化，使其具有单位范数。
    • 所有特征向量存储在一个列表中，并最终转换为NumPy数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
def get_features(image, x, y, feature_width):

    #normalized patches

    # # 存储所有特征描述符的列表
    # all_descriptors = []
    #
    # # 遍历每个兴趣点的坐标
    # for i in range(len(x)):
    #     # 获取当前兴趣点的坐标
    #     point_x = x[i]
    #     point_y = y[i]
    #
    #     # 提取当前兴趣点周围的图像块
    #     patch = image[int(point_y) - feature_width // 2: int(point_y) + feature_width // 2,
    #             int(point_x) - feature_width // 2: int(point_x) + feature_width // 2]
    #
    #     # 将图像块归一化为0到1的范围
    #     normalized_patch = patch.astype(float) / 255.0
    #
    #     # 将归一化的图像块展平为一维数组
    #     flattened_patch = normalized_patch.flatten()
    #
    #     # 将展平后的图像块作为特征描述符
    #     all_descriptors.append(flattened_patch)
    #
    # # 将特征描述符转换为 numpy 数组
    # features = np.array(all_descriptors)




    # SIFT -------

    features = []
    num_bins = 8
    cell_width = feature_width // 4

    # Gaussian smoothing to reduce noise
    smoothed_image = gaussian(image, sigma=1, mode='reflect')

    # Iterate over interest points
    for i in range(len(x)):
        # Extract patch around interest point
        patch = smoothed_image[int(y[i] - feature_width / 2):int(y[i] + feature_width / 2),
                int(x[i] - feature_width / 2):int(x[i] + feature_width / 2)]

        # Divide patch into 4x4 cells
        cells = np.split(patch, 4, axis=0)
        cells = [np.split(cell, 4, axis=1) for cell in cells]

        # Compute gradients and orientations for each cell
        cell_gradients = []
        for row in cells:
            for cell in row:
                # Compute gradients using Sobel filters
                gradient_x = np.gradient(cell)[1]
                gradient_y = np.gradient(cell)[0]

                # Compute gradient magnitude and orientation
                gradient_magnitude = np.sqrt(gradient_x ** 2 + gradient_y ** 2)
                gradient_orientation = np.arctan2(gradient_y, gradient_x)

                # Bin orientations into histogram
                histogram, _ = np.histogram(gradient_orientation, bins=num_bins, range=(-np.pi, np.pi),
                                            weights=gradient_magnitude)
                cell_gradients.append(histogram)

        # Concatenate histograms to form feature vector
        feature_vector = np.concatenate(cell_gradients)

        # Normalize feature vector
        feature_vector /= np.linalg.norm(feature_vector)

        features.append(feature_vector)


    features = np.array(features)


    return features
3. match_features()
  1. 计算特征间距离：
    • 使用numpy的linalg.norm函数计算两组特征描述符之间的欧氏距离。这会生成一个矩阵，其中每个元素表示第一幅图像中一个特征与第二幅图像中所有特征之间的距离。
  2. 找到最佳匹配：
    • 对于第一幅图像中的每个特征，找到与之距离最近的特征在第二幅图像中的索引（即最佳匹配）。
    • 找到第二幅图像中每个特征的次优匹配。
  3. 应用最近邻距离比（NNDR）测试：
    • 计算最佳匹配与次优匹配之间的距离比率。
    • 根据设定的阈值（这里是0.8），判断最佳匹配是否“好”的。如果最佳匹配的距离比率小于0.8，则认为这是一个好的匹配。
  4. 生成匹配结果：
    • 将所有“好”的匹配结果保存在一个数组中，其中每一对匹配是一行，包含第一幅图像中的特征索引和第二幅图像中的特征索引。
    • 生成与匹配相对应的置信度值，这里用1减去距离比率。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def match_features(im1_features, im2_features):
    # matrix ----------------------------------
    matches = []
    confidences = []

    # Calculate distances between all pairs of feature descriptors
    distances = np.linalg.norm(im1_features[:, np.newaxis, :] - im2_features, axis=2)

    # Find the best and second best matches for each feature in im1
    best_match_indices = np.argmin(distances, axis=1)
    best_match_distances = distances[np.arange(len(im1_features)), best_match_indices]
    distances[np.arange(len(im1_features)), best_match_indices] = np.inf
    second_best_match_distances = np.min(distances, axis=1)

    # Apply NNDR test
    ratio = best_match_distances / second_best_match_distances
    good_matches = ratio < 0.8
    matches = np.column_stack((np.nonzero(good_matches)[0], best_match_indices[good_matches]))
    confidences = 1 - ratio[good_matches]

    return matches, confidences

2. SIFT 对比normalized patches的提升

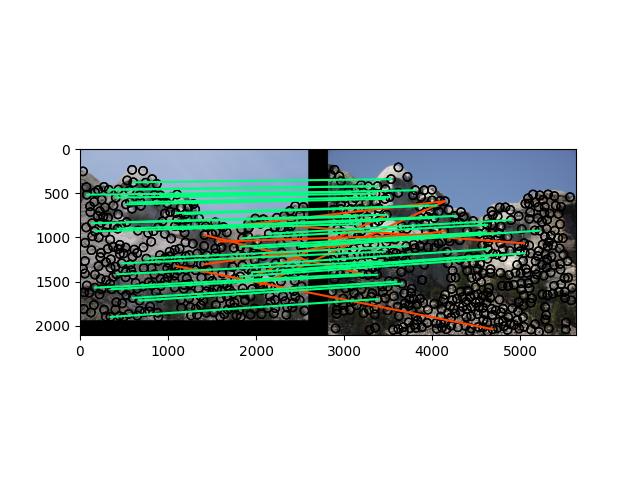
对于mt_rushmore，

使用normalized patches：

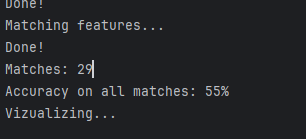
image-20240505215216893.png

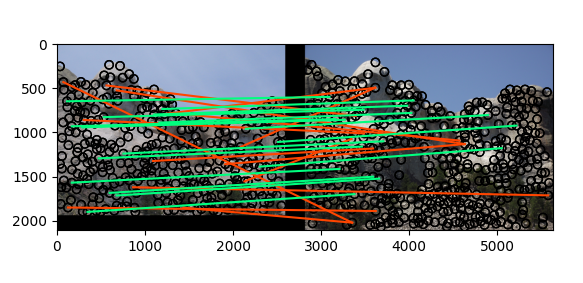
image-20240505215207809.png

使用SIFT：

image-20240505215103631.png

image-20240505215049894.png

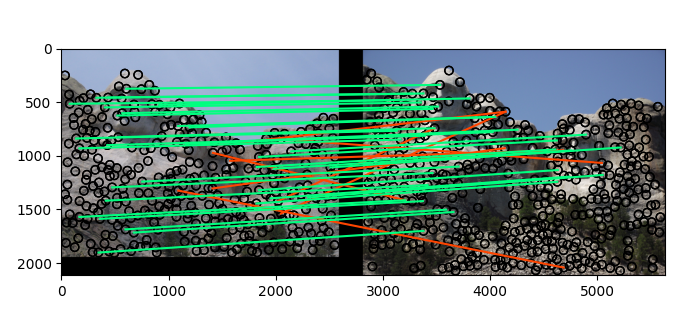
使用SIFT之后，识别的准确率从 55%上升到了80%

3.结果

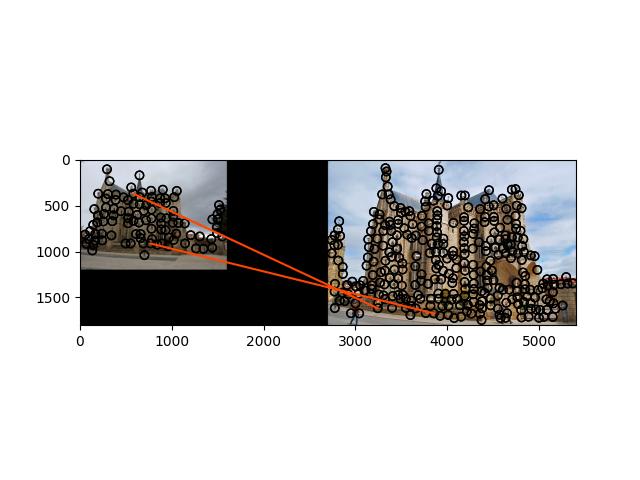
1.notre_dame

image-20240505215617683.png

2.mt_rushmore

mt_rushmore_matches.jpg

image-20240505215553314.png

3.e_gaudi

e_gaudi_matches.jpg

Morty

Morty

我阐释你的梦

7
2
6
TOC
  1. 1. 图像处理lab2
    1. 1.1. 1.Questions
    2. 1.2. 2.Programming
NOTICE

看到这条通知的请立即微信转账50块，收到扣1

CATEGORYS
TAGS
CV Parallel Programming RAID gpt hexo mamba